짜리몽땅 매거진
[금융 AI] AI 기반 금융 사기 탐지(3) - Isolation Forest 기반 신용카드 사기 거래 탐지 모델 본문
[금융 AI] AI 기반 금융 사기 탐지(3) - Isolation Forest 기반 신용카드 사기 거래 탐지 모델
쿡국 2025. 4. 19. 08:02금융 사기 거래 탐지는 끊임없이 진화하는 사기꾼들과의 지능적인 싸움과 같다. 새로운 패턴을 학습하고 대응 방안을 찾는 동안 사기꾼들도 사기 방법을 지속적으로 변화시킨다. 이러한 상황에서는 기존의 접근 방식만으로는 충분하지 않다. 특히 사기 거래의 패턴이 빠르게 변화하고, 레이블링된 데이터가 부족한 상황에서는 더욱 그렇다. 따라서 사기의 새로운 패턴을 빠르게 감지하고 효과적으로 대응할 수 있는 새로운 기술과 방법론을 모색해야 한다.
지난 SMOTE 및 XGBoost 기반 모델에 이어 이번에는 Isolation Forest 기반 신용카드 사기 거래 탐지 모델링 실습을 진행해보자. Isolation Forest 알고리즘에 대한 설명은 지난 포스팅을 참고하자.
[Python] 데이터에서의 Outlier 처리
데이터 전처리에는 여러 과정이 포함되지만, 그 중에서도 이상치(Outlier) 처리는 매우 중요한 단계이다. 이상치란 일반적인 데이터 패턴에서 벗어난 값으로, 종종 잘못된 데이터 입력이나 측정
zzarimongddang.tistory.com
위 글에는 간단히 설명되어 있기 때문에, 이번 기회에 Isolation Forest 알고리즘에 대한 설명을 한 번 더 짚고 넘어가보자.
일련의 1차원 데이터가 주어졌다고 가정해보자. 이 데이터 안에는 A와 B라는 두 개의 데이터 포인트가 있다. 우리의 목표는 이 두 데이터 포인트를 다른 데이터들로부터 분리하는 것이다. 그럼 어떻게 이것을 할 수 있을까? 우리는 데이터의 최대값과 최소값 사이에서 임의의 값 X를 선택하고, 이 값 X를 기준으로 데이터를 두 그룹(<X 와 >=X)으로 분리한다. 그 다음 이 두 그룹을 또 다시 같은 방법으로 분리하고, 이런 식으로 계속해서 데이터를 분리해 나간다. 이렇게 하면서 데이터가 더 이상 분리되지 않을 때까지 계속한다.
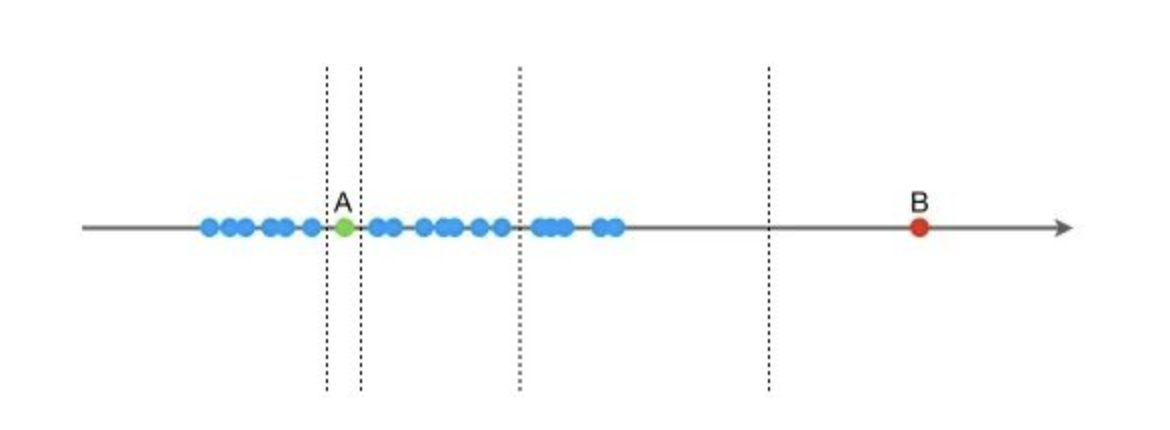
이 과정에서 주목할 점은, B는 다른 데이터로부터 비교적 멀리 떨어져 있기 때문에 이를 분리하는 데 필요한 분리 횟수가 매우 적다는 것이다. 반면에 A는 다른 데이터 포인트와 군집을 이루고 있으므로, A를 분리하는 데는 많은 분리 횟수가 필요하다.
이런 방식으로 Isolation Forest 알고리즘은 분리 횟수를 통해 데이터 포인트가 군집에 속해 있는지(정상), 아니면 고립되어 있는지(이상치)를 판별한다. 즉, 분리 횟수가 적을수록 데이터 포인트는 이상치일 가능성이 높고, 분리 횟수가 많을수록 데이터 포인트는 정상 데이터일 가능성이 높다.
이것이 바로 Isolation Forest 알고리즘이 이상치를 어떻게 찾아내는지에 대한 간단한 예시이다. 이러한 방법을 통해 Isolation Forest는 높은 차원의 데이터에서도 효과적으로 이상치를 탐지할 수 있다. 이상치를 고립된 나무로 생각하고, 분리 횟수를 이용하여 이상치를 판별하는 방식이 이 알고리즘의 핵심이다.
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
from sklearn.ensemble import IsolationForest
data = pd.read_csv('creditcard.csv')
필요 라이브러리를 호출하고, 지난 실습과 동일하게 creditcard 데이터를 불러온다.
num_nonfraud = np.sum(data['Class'] == 0)
num_fraud = np.sum(data['Class'] == 1)
plt.bar(['Fraud', 'Non-Fraud'], [num_fraud, num_nonfraud], color=['red', 'lightgrey'])
plt.title('Number of Fraud vs Non-Fraud Transactions', fontsize=14)
plt.xlabel('Transaction Type', fontsize=12)
plt.ylabel('Count', fontsize=12)
for i, value in enumerate([num_fraud, num_nonfraud]):
plt.text(i, value, str(value), ha='center', va='bottom', fontsize=11, fontweight='bold')
plt.style.use('seaborn-whitegrid')
plt.show()
Class 칼럼의 분포를 바차트로 시각화하여 확인한다.
data['Hour'] = data["Time"].apply(lambda x : divmod(x, 3600)[0])
X = data.drop(['Time','Class'],axis=1)
Y = data.Class
# 모델 훈련
iforest = IsolationForest()
# fit_predict 함수로 훈련 및 예측을 동시에 수행하여 모델에서의 이상치 여부를 판단합니다. -1은 이상치, 1은 정상을 의미합니다.
data['label'] = iforest.fit_predict(X)
# decision_function을 사용하여 예측을 통해 이상치 점수를 얻을 수 있습니다.
data['scores'] = iforest.decision_function(X)
# TopN 정확도 평가
n = 1000
df = data.sort_values(by='scores', ascending=True)
df = df.head(n)
rate = df[df['Class'] == 1].shape[0] / n
print('Top{}의 정확도는: {}'.format(n, rate))
-->Top1000의 정확도는: 0.137
데이터 분할 후, Isolation Forest 알고리즘을 통해 훈련 및 예측을 동시에 수행하여 모델의 이상치 여부를 판단한다. 근데 정확도가 0.137로 낮게 나온 것을 확인할 수 있다. 이를 위해 Isolation Forest의 기존 파라미터 값을 확인한 후 하이퍼파라미터 튜닝 작업을 수행한다.
iforest.get_params()
-->
{'bootstrap': False,
'contamination': 'auto',
'max_features': 1.0,
'max_samples': 'auto',
'n_estimators': 100,
'n_jobs': None,
'random_state': None,
'verbose': 0,
'warm_start': False}
1) n_estimators 조정
import warnings
import matplotlib.pyplot as plt
warnings.filterwarnings('ignore')
n_est = list(range(10, 500, 10))
rates = []
for i in n_est:
# 모델 훈련
iforest = IsolationForest(n_estimators=i,
max_samples=256,
contamination=0.02,
max_features=5,
random_state=1
)
# fit_predict 함수로 모델 훈련 및 예측
data['label'] = iforest.fit_predict(X)
# decision_function으로 이상치 점수 예측
data['scores'] = iforest.decision_function(X)
# TopN 정확도 평가
n = 1000
df = data.sort_values(by='scores', ascending=True)
df = df.head(n)
rate = df[df['Class']==1].shape[0] / n
print('Top{}의 정확도: {}'.format(n, rate))
rates.append(rate)
# 그래프 그리기
plt.style.use('seaborn-whitegrid')
plt.plot(n_est, rates, linestyle='--', marker='.', color='c', markerfacecolor='red')
plt.xlabel('n_estimators')
plt.ylabel('정확도')
plt.title('The impact of n_estimators on the accuracy of outlier detection')
# 그래프 표시
plt.show()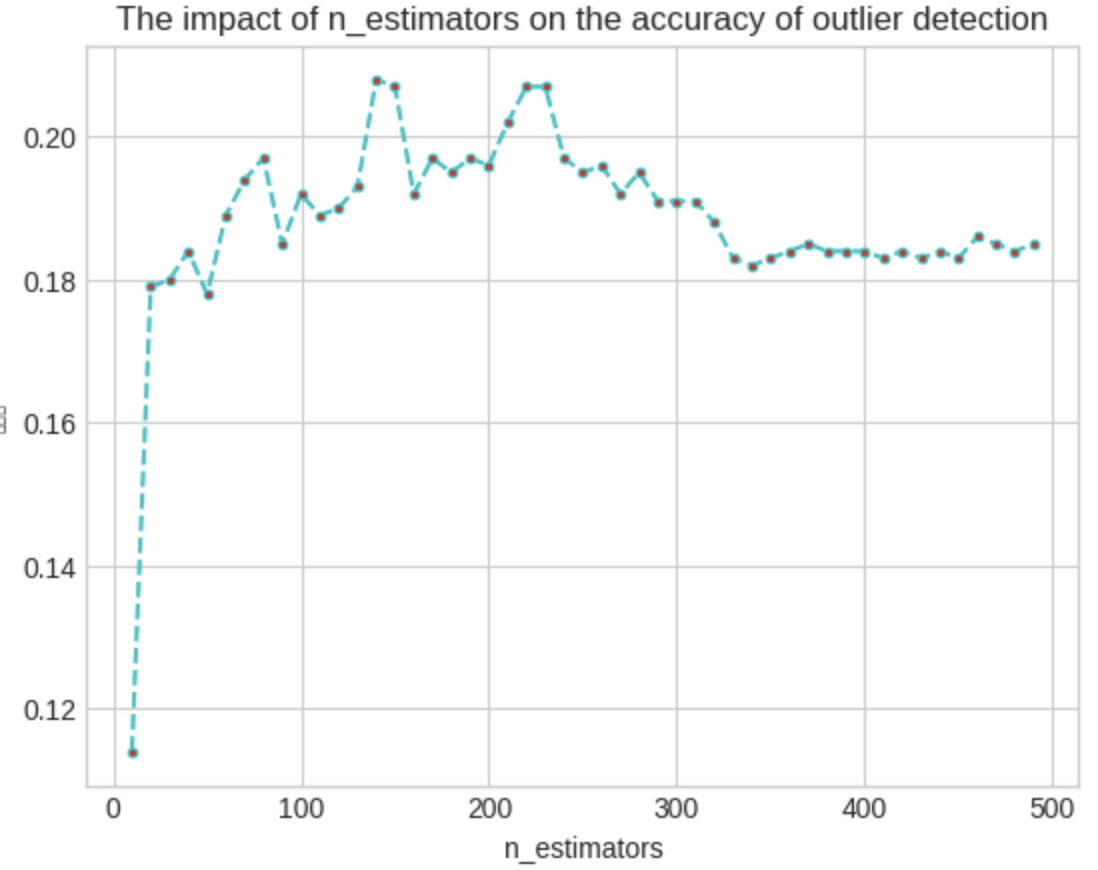
그래프에서 볼 수 있듯이, 나무의 개수가 200을 초과하면 정확도가 감소하기 시작한다. 약 300개의 나무에서는 상당히 낮은 수준에서 안정화되며 큰 개선이 나타나지 않는다. 따라서, 나무의 개수가 많다고 해서 항상 더 좋은 성능을 보장하는 것은 아닌 것을 알 수 있다.
2) max_samples 조정
# 샘플 크기 범위를 정의
samples = list(range(50,270000,2000))
# 정확도를 저장할 빈 리스트를 생성합니다.
rates = []
# 각 샘플 크기에 대해 반복
for i in samples:
# 모델을 학습시킵니다.
iforest = IsolationForest(n_estimators=100,
max_samples = i,
contamination=0.02,
max_features=5,
random_state=1
)
# fit_predict 함수를 사용하여 데이터를 학습하고 예측. 이상치는 -1, 정상은 1로 표시.
data['label'] = iforest.fit_predict(X)
# decision_function을 사용하여 이상치 점수를 계산.
data['scores'] = iforest.decision_function(X)
# TopN 정확도를 평가.
n = 1000
# 점수가 낮은 순서대로 데이터를 정렬.
df = data.sort_values(by='scores',ascending=True)
# Top N 데이터를 선택.
df = df.head(n)
# 선택된 데이터 중 이상치의 비율을 계산.
rate = df[df['Class']==1].shape[0]/n
print('Top{}의 정확도:{}'.format(n,rate))
# 정확도를 rates 리스트에 추가.
rates.append(rate)
# 결과를 그래프로 시각화.
import matplotlib.pyplot as plt
plt.plot(samples,rates, linestyle='--', marker='.',color='c',markerfacecolor='red')
plt.title('max_samples and TopN Acc')
plt.show()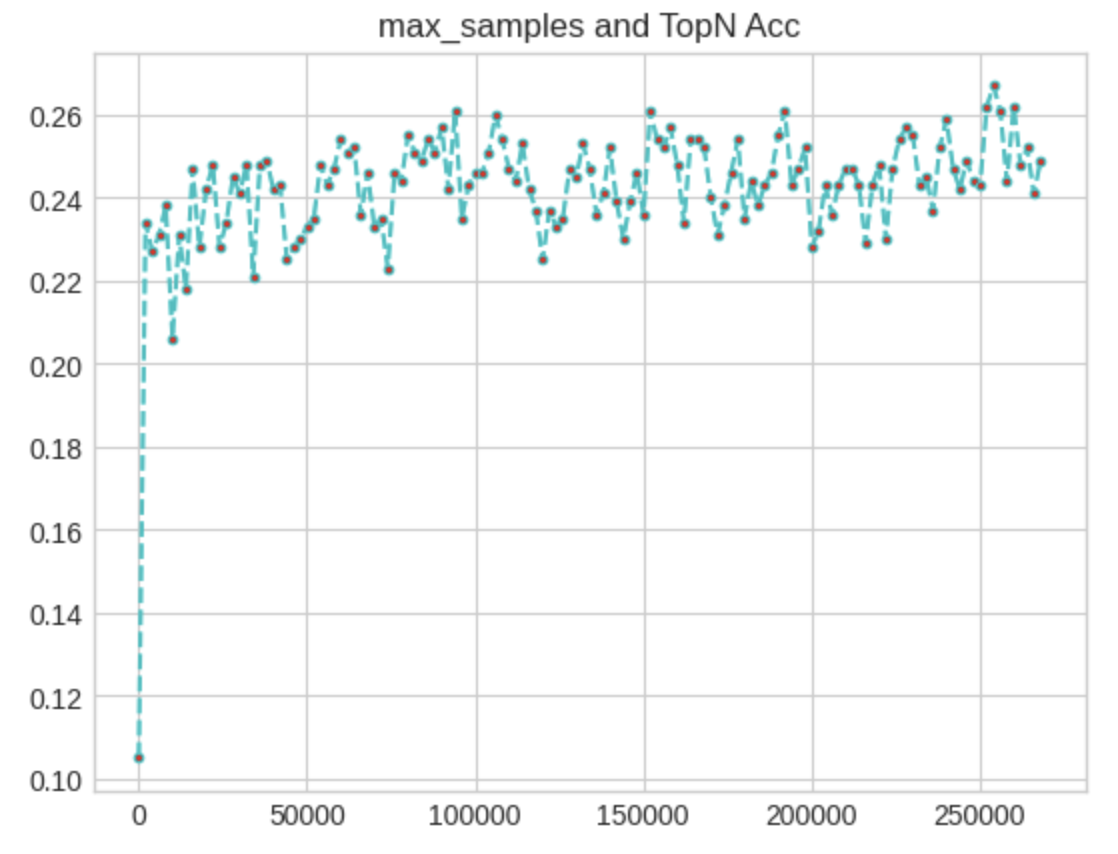
범위를 25만까지 늘리니 정확도가 0.26 선에서 형성되는 것을 확인할 수 있다.
3) max_features 조정
features = list(range(1, X.shape[1]+1))
rates = []
for i in features:
# 모델 훈련
iforest = IsolationForest(n_estimators=100,
max_samples=1200,
contamination=0.02,
max_features=i,
random_state=1
)
# fit_predict 함수로 훈련 및 예측을 동시에 수행하여 모델에서의 이상치 여부를 판단합니다. -1은 이상치, 1은 정상을 의미합니다.
data['label'] = iforest.fit_predict(X)
# decision_function을 사용하여 예측을 통해 이상치 점수를 얻을 수 있습니다.
data['scores'] = iforest.decision_function(X)
# Top-N 정확도 평가
n = 1000
df = data.sort_values(by='scores', ascending=True)
df = df.head(n)
rate = df[df['Class'] == 1].shape[0] / n
print('Top{}의 정확도는: {}'.format(n, rate))
rates.append(rate)
print(features)
# [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30]
print(rates)
# [0.198, 0.195, 0.188, 0.191, 0.192, 0.185, 0.184, 0.161, 0.158, 0.166, 0.209, 0.183, 0.174, 0.169, 0.164, 0.154, 0.167, 0.17, 0.183, 0.149, 0.186, 0.18, 0.183, 0.195, 0.187, 0.157, 0.191, 0.189, 0.146, 0.23]
import matplotlib.pyplot as plt
plt.plot(features, rates, linestyle='--', marker='.', color='c', markerfacecolor='red')
plt.title('max_features and Top-N Accuracy')
plt.xlabel('max_features')
plt.ylabel('Accuracy')
plt.show()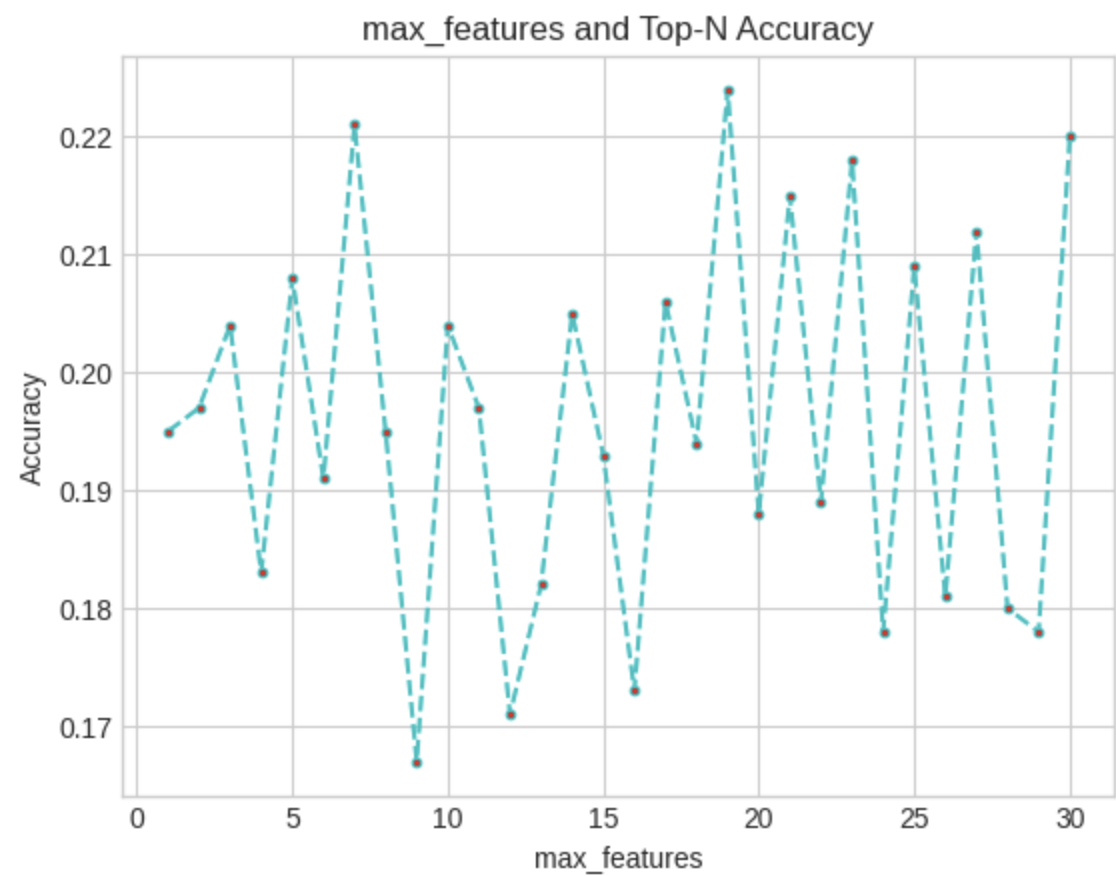
특성이 많을 때 정확도가 높을 때도 있지만, 이론적으로 이는 크게 가능하지 않는다. 랜덤 포레스트를 연구할 때 알 수 있듯이, 특성이 최대일 때 모델의 상관성이 매우 높아져, 통합 정확도가 오히려 떨어진다. 그렇다면 왜 이런 상황이 발생하는 것일까? 추출하는 샘플의 수가 기존에는 100으로 너무 적기 때문이라고 추측한다. 샘플 수를 1200정도까지 늘려서 다시 살펴보니 대략 7정도의 값에서 좋은 성능을 얻을 수 있었다.
4) Final Test
# 모델 훈련
iforest = IsolationForest(n_estimators=250,
max_samples = 125000,
contamination=0.05,
max_features=5,
random_state=1
)
# fit_predict 함수를 이용해 훈련과 예측을 함께 수행하며, -1은 이상치, 1은 정상치를 나타냄
data['label'] = iforest.fit_predict(X)
# decision_function을 이용해 이상치 점수를 예측
data['scores'] = iforest.decision_function(X)
# TopN 정확도 평가
n = 1000
df = data.sort_values(by='scores',ascending=True)
df = df.head(n)
rate = df[df['Class']==1].shape[0]/n
print('Top{}의 정확도는:{}'.format(n,rate))
# 출력 결과: Top1000의 정확도는:0.251
이와 같이 파라미터 조정을 통해 다시 테스트를 진행하니 기존의 13%정도의 정확도가 25%까지 상승한 것을 확인할 수 있다.
'Data > Financial AI' 카테고리의 다른 글
| [금융 AI] AI 기반 금융 사기 탐지(5) - Networkx 라이브러리 기반 커뮤니티 탐지 (1) | 2025.05.05 |
|---|---|
| [금융 AI] AI 기반 금융 사기 탐지(4) - AutoEncoder 기반 신용카드 사기 거래 탐지 모델 (0) | 2025.05.01 |
| [금융 AI] AI 기반 금융 사기 탐지(2) - SMOTE & XGBoost 기반 신용카드 사기 거래 탐지 모델 (0) | 2025.04.17 |
| [금융 AI] AI 기반 금융 사기 탐지(1) - 금융 사기 거래 탐지의 중요성과 AI (0) | 2025.04.14 |
| [금융 AI] AI 기반의 신용 리스크 모델링(5) - QnA (0) | 2025.04.10 |


